
The terms scientists use to describe what they study can seem arbitrary. It may seem as though words they use are only words with nothing else to them. But studying the terms scientists use to describe various phenomena lets you better understand the meaning behind them.
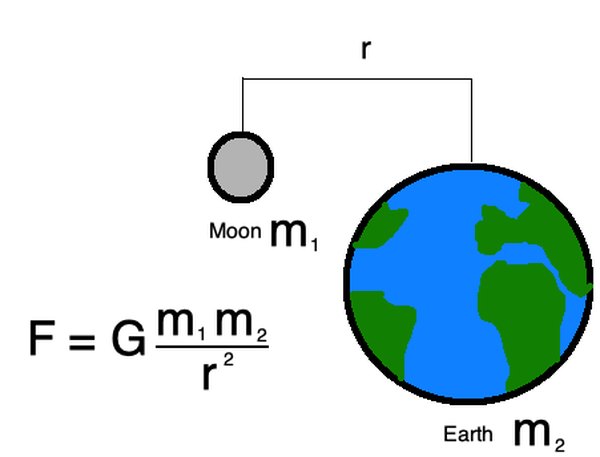
Newton's law of universal gravitation demonstrates the universalizable, common nature of laws that describe nature and the universe.
Physics Laws and Principles
The differences between terminology in the meaning of a physics law and principles of physics can be confusing.
Tips
Laws are general rules and ideas that adhere to the nature of the universe while principles describe specific phenomena that require clarity and explanation. Other terms like theorems, theories, and rules can describe nature and the universe. Understanding the differences between these terms in physics can improve your rhetoric and language when speaking about science.
A law is an important insight about the nature of the universe. A law can be experimentally verified by taking into account observations about the universe and asking what general rule governs them. Laws may be one set of criteria for describing phenomena such as Newton's first law (an object will remain at rest or move at a constant velocity motion unless acted upon by an external force) or one equation such as Newton's second law (F = ma for net force, mass, and acceleration).
Laws are deduced through lots of observations and accounting for various possibilities of competing hypotheses. They don't explain a mechanism by which a phenomena occurs, but, rather, describe these numerous observations. Whichever law can best account for these empirical observations by explaining phenomena in a general, universalized manner is the law that scientists accept. Laws are applied to all objects regardless of scenario but they are only meaningful within certain contexts.
A principle is a rule or mechanism by which specific scientific phenomena work. Principles typically have more requirements or criteria when it can be used. They generally require more explanation to articulate as opposed to a single universal equation.
Principles can also describe specific values and concepts such as entropy or Archimedes principle, which relates buoyancy to the weight of displaced water. Scientists typically follow a method of identifying a problem, collecting information, forming and testing hypotheses and drawing conclusions when determining principles.
Examples of Scientific Principles in Everyday Life
Principles can also be general ideas that govern disciplines such as cell theory, gene theory, evolution, homeostasis, and laws of thermodynamics being a scientific principle definition in biology They're involved in a variety of phenomena in biology and, instead of providing a definite, universal feature of the universe, they're meant to further theories and research in biology.
There are other examples of scientific principles in everyday life. It's impossible to distinguish between a gravitational force and the inertial force, the force to accelerate an object, known as the principle of equivalence. It tells you that if you're in an elevator in free fall, you wouldn't be able to measure the gravitational force because you couldn't distinguish between it and the force that pulls you in the direction opposite to gravity.
Newton's Three laws of Motion
Newton's first law, that an object in motion will remain in motion until acted upon by an external force, means objects that have no net force (the sum of all forces on an object) will not experience acceleration. It will either remain at rest or move with a constant velocity, the direction and speed of an object. It's very central and common to many phenomena in how it connects the motion of an object with the forces that act upon it no matter whether it's a celestial body or a ball resting on the ground.
Newton's second law, F = ma, lets you determine the acceleration or mass from this net force for these objects. You can calculate the net force due to gravity of a falling ball or a car making a turn. This fundamental feature of physical phenomena makes it a universalized law.
Newton's third law illustrates these features as well. Newton's third law states that for every action, there is an equal and opposite reaction. The statement means that in every interaction, there is a pair of forces acting on the two interacting objects. When the sun pulls the planets towards it as they orbit, the planets pull back in response, These laws of physics describe these features of nature as inherent within the universe.
Principles of Physics
Heisenberg's Uncertainty Principle can be described as "nothing has a definite position, a definite trajectory, or a definite momentum," but it also requires further explanation for clarity. When physicist Werner Heisenberg tried studying subatomic particles with increased precision, he found it impossible to exactly determine a particle's momentum and position simultaneously.
Heisenberg used the German word "Ungenauigkeit," meaning "imprecision" not "uncertainty" to describe this phenomena that we would call the Uncertainty Principle. The momentum, the product of an object's velocity and mass, and position are always at a tradeoff between one another.
The original German word describes the phenomena more accurately than the word "uncertainty" does. The Uncertainty Principle adds uncertainty to observations based on the imprecision of a physicist's scientific measurements. Because these principles depend highly on the context and conditions of the principle, they are more like guiding theories used to make predictions about the universe phenomena than laws are.
If a physicist studied the motion of an electron in a large box, she could get a fairly accurate idea of how it would travel throughout the box. But if the box were made smaller and smaller such that the electron couldn't move, we would know more about where the electron is, but know much less about how fast it was traveling. For objects in our every day life, such as a moving car, you can determine the momentum and position, but there would still be a very small amount of uncertainty with these measurements because the uncertainties are much more significant for particles than everyday objects.
Other Terms
While laws and principles describe these two different ideas across physics, biology and other disciplines, theories are collections of concepts, laws and ideas to explain observations of the universe. The theory of evolution and the the general theory of relativity describe how species have changed over generations and how massive objects distort space-time through gravity, respectively.
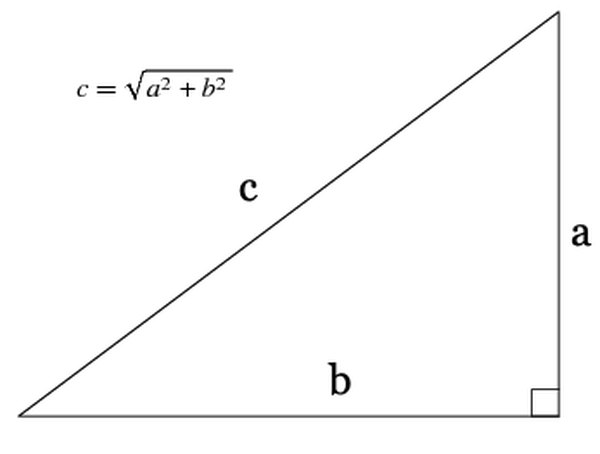
In mathematics, researchers can refer to theorems, mathematical claims that can be proven or disproven, and lemmas, less important results usually used as steps to prove theorems. The Pythagorean theorem depends on the geometry of a right triangle to determine the length of their sides. It can be proven mathematically.
If x and y are any two whole numbers such that a = x2 − y2, b = 2xy, and c = x2 + y2, then:
- a2 + b2 = (x2 − y2)2 + (2xy)2
- a2 + b2 = x4 − 2x2y2 + x4 + 4x2y2
- a2 + b2 = x4 + 2x2y2 + x4
- a2 + b2 = (x2 + y2)2 = c2
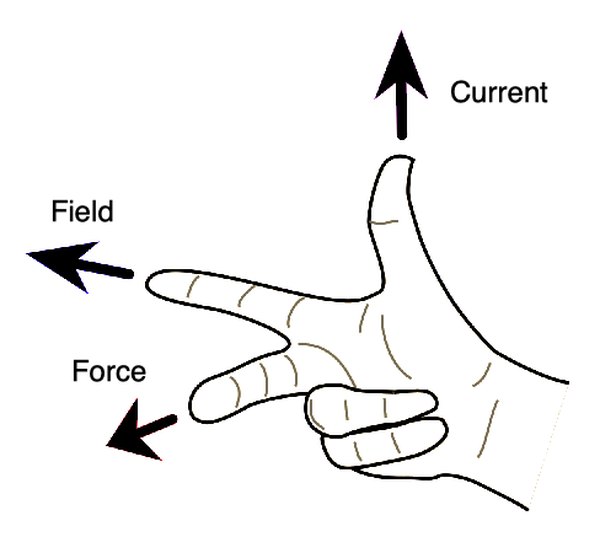
Other terms may not be as clear. The difference between a rule and a principle may be debated, but rules generally refer to how to determine the correct answer from different possibilities. The right-hand rule lets physicists determine how electric current, magnetic field, and magnetic force depend on the direction of each other. Though it's based on fundamental laws and theories of electromagnetism, it's more used as a general "rule of thumb" in solving equations in electricity and magnetism.
Examining the rhetoric behind how scientists communicate tells you more about what they mean when they describe the universe. Understanding the use of these terms is pertinent to understanding their true meaning.
References
About the Author
S. Hussain Ather is a Master's student in Science Communications the University of California, Santa Cruz. After studying physics and philosophy as an undergraduate at Indiana University-Bloomington, he worked as a scientist at the National Institutes of Health for two years. He primarily performs research in and write about neuroscience and philosophy, however, his interests span ethics, policy, and other areas relevant to science.
